 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
配点 : 1900 点
問題文
N 頂点の木があります。 頂点は 1 から N まで番号が振られています。 各 1 ≤ i ≤ N - 1 について、i 番目の辺は頂点 a_i と b_i を繋いでいます。 辺の長さはすべて 1 です。
いくつかの頂点はすぬけ君のお気に入りです。
お気に入りの頂点の情報は、長さ N の文字列 s として与えられます。
各 1 ≤ i ≤ N について、頂点 i がお気に入りならば s_i は 1 で、頂点 i がお気に入りでないならば s_i は 0 です。
最初、頂点はすべて白色です。 すぬけ君は次の操作をちょうど 1 回だけ行います。
- お気に入りの頂点 v をひとつ選び、非負整数 d をひとつ選ぶ。 頂点 v から距離 d 以内の頂点をすべて黒く塗る。
最終的な頂点の色の組合せとして考えられるものは何通りか求めてください。
制約
- 2 ≤ N ≤ 2×10^5
- 1 ≤ a_i, b_i ≤ N
- グラフは木である。
- |s| = N
- s は
0と1のみからなる。 - s には
1が含まれる。
部分点
- 1300 点分のデータセットでは、s は
1のみからなる。
入力
入力は以下の形式で標準入力から与えられる。
N
a_1 b_1
a_2 b_2
:
a_{N - 1} b_{N - 1}
s
出力
最終的な頂点の色の組合せとして考えられるものは何通りか出力せよ。
入力例 1
4 1 2 1 3 1 4 1100
出力例 1
4
次の 4 通りです。
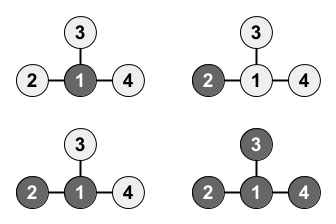
入力例 2
5 1 2 1 3 1 4 4 5 11111
出力例 2
11
このケースは部分点の制約を満たします。
入力例 3
6 1 2 1 3 1 4 2 5 2 6 100011
出力例 3
8
Score : 1900 points
Problem Statement
There is a tree with N vertices. The vertices are numbered 1 through N. For each 1 ≤ i ≤ N - 1, the i-th edge connects vertices a_i and b_i. The lengths of all the edges are 1.
Snuke likes some of the vertices.
The information on his favorite vertices are given to you as a string s of length N.
For each 1 ≤ i ≤ N, s_i is 1 if Snuke likes vertex i, and 0 if he does not like vertex i.
Initially, all the vertices are white. Snuke will perform the following operation exactly once:
- Select a vertex v that he likes, and a non-negative integer d. Then, paint all the vertices black whose distances from v are at most d.
Find the number of the possible combinations of colors of the vertices after the operation.
Constraints
- 2 ≤ N ≤ 2×10^5
- 1 ≤ a_i, b_i ≤ N
- The given graph is a tree.
- |s| = N
- s consists of
0and1. - s contains at least one occurrence of
1.
Partial Score
- In the test set worth 1300 points, s consists only of
1.
Input
The input is given from Standard Input in the following format:
N
a_1 b_1
a_2 b_2
:
a_{N - 1} b_{N - 1}
s
Output
Print the number of the possible combinations of colors of the vertices after the operation.
Sample Input 1
4 1 2 1 3 1 4 1100
Sample Output 1
4
The following four combinations of colors of the vertices are possible:

Sample Input 2
5 1 2 1 3 1 4 4 5 11111
Sample Output 2
11
This case satisfies the additional constraint for the partial score.
Sample Input 3
6 1 2 1 3 1 4 2 5 2 6 100011
Sample Output 3
8